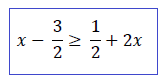01) Se na figura abaixo, ∆ ABC ≡ ∆ EDC, então x + y é
igual a:
(A) 3
(B) 6
(C) 9
(D) 18
Resposta: C
Resolução:
2x + 5 = 11 3y - 6 = 12
2x = 11 - 5 3y = 12 + 6
2x = 6 3y = 18
x = 6/2 y = 18/3
x = 3 y = 6
x + y
3 + 6 = 9
Resolução:
2x + 5 = 11 3y - 6 = 12
2x = 11 - 5 3y = 12 + 6
2x = 6 3y = 18
x = 6/2 y = 18/3
x = 3 y = 6
x + y
3 + 6 = 9
02) O número de triângulo isósceles não congruentes que podem ser construídos, medindo um dos ângulos 50°, é:
(A) 1
(B) 2
(C) 3
(D) 4
Resposta: B
03) Um triângulo isósceles é tal que a medida do ângulo adjacentes à base é terça parte da medida do ângulo oposto à base. O menor ângulo desse triângulo mede:
(A) 28°
(B) 36°
(C) 40°
(D) 42°
Resposta: B
Resolução: x + x/3 + x/3 = 180º ângulo maior = x = 108°
x + 2x/3 = 180° os dois ângulos menor x/3 =
3x + 2x = 540° 108°/3 = 36°
5x = 540°
x = 540°/5
x = 108°
Resolução: x + x/3 + x/3 = 180º ângulo maior = x = 108°
x + 2x/3 = 180° os dois ângulos menor x/3 =
3x + 2x = 540° 108°/3 = 36°
5x = 540°
x = 540°/5
x = 108°
04) O perímetro de um triângulo isósceles de base BC é 35 cm. Se AS é uma bissetriz e SC = 8 cm, então a medida de AB é:
(A) 7,5 cm.
(B) 8,5 cm.
(C) 9,5 cm.
(D) 9,8 cm.
Resposta: C
Resolução: 2x + 16 = 35
2x = 35 - 16
2x = 19
x = 19/2
x = 9,5
Resolução: 2x + 16 = 35
2x = 35 - 16
2x = 19
x = 19/2
x = 9,5
05) Em um triângulo isósceles a média aritmética das medidas de dois de seus ângulos é 50°.
A medida de um dos ângulos do triângulo pode ser:
(A) 90°
(B) 60°
(C) 30°
(D) 20°
Resposta: D
Resolução:
50 = (a + a)/2
a = 50º
Assim o outro ângulo seria
180-2.50 = b
b = 80º
Ou que um seja o dos congruentes e o outro o ângulo diferente.
50 = (a + b)/2
100 = a+b
Sabemos que a soma dos ângulos internos do triângulo é igual a 180º.
Assim:
a+a+b = 180
Como a+b = 100
a+100 = 180
a = 80º
Assim o outro ângulo seria.
a+b = 100
80 + b = 100
b = 20º
Resolução:
Que esses dois ângulos sejam os ângulos
congruentes do triângulo. Logo:
50 = (a + a)/2
a = 50º
Assim o outro ângulo seria
180-2.50 = b
b = 80º
Ou que um seja o dos congruentes e o outro o ângulo diferente.
50 = (a + b)/2
100 = a+b
Sabemos que a soma dos ângulos internos do triângulo é igual a 180º.
Assim:
a+a+b = 180
Como a+b = 100
a+100 = 180
a = 80º
Assim o outro ângulo seria.
a+b = 100
80 + b = 100
b = 20º