A probabilidade de a carta retirada ter a figura de uma pessoa é:
2) As cinco cartelas numeradas representadas a seguir foram colocadas numa caixa.
Se forem retiradas duas cartelas da caixa, simultaneamente e ao acaso, a probabilidade
de que a soma dos valores das cartelas retiradas seja 5 ou 6 é:
3) Na linha representada no sistema de eixos abaixo descreve a rota de um avião no radar.
Como o avião voa em linha reta ( entre as longitudes 0° e 60° ), a cada grau de longitude
é possível se prever a latitude em que o avião estará. Se chamarmos de x a longitude e de
y a latitude, a equação que descreve a rota do avião no radar é dada por:
a) y = 2x + 10
b) y = x – 20
c) y = 2x – 20
d) y = 2x + 20
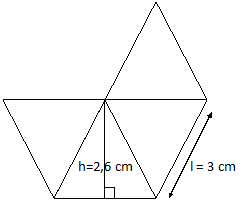
4) A figura a seguir é composta de triângulos equiláteros de lado l = 3 cm. Se adotarmos
que estes triângulos têm altura aproximada de 2,6 cm, a área total da figura será de
aproximadamente.
a) 14,4 cm²
b) 15,6 cm²
c) 16,5 cm²
d) 17,2 cm²
5) As questões de uma prova são avaliadas por pontos, de modo que um acerto vale 5
pontos positivos e um erro vale três pontos negativos. Em uma prova com 30
questões, Mirella fez 54 pontos. Quantas questões Mirella acertou ?
Para resolver o problema, o professor denominou x e y ao número de questões
acertadas e erradas por Mirella, respectivamente, e pediu aos alunos que escrevessem o
sistema de equações que conduz à solução do problema.
Assinale a alternativa que mostra corretamente o sistema de equações pedido pelo:
6) Num campeonato de futebol, os times ganham 3 pontos em cada vitória, 1 ponto por
empate e 0 ponto por derrota. O time Cruzadão participou de 50 jogos e fez 54 pontos,
tendo perdido 12 jogos. Chame de v o número de jogos que Cruzadão venceu d, o
número de jogos em que foi derrotado e e, os jogos em que houve empate.Assinale a
alternativa que mostra corretamente o sistema de equações que representa essa
situação:
7) Represente no sistema cartesiano os pontos M(–1,2), N(2,1), P(–1,–3) e Q(3,1).
Dentre estes pontos, o mais distante do ponto (3, –4) é:
a) M.
b) N.
c) P.
d) Q.
8) Uma menina recortou vários triângulos equiláteros iguais em cartolina. Resolveu
então construir poliedros com aqueles triângulos, colando-os com fita adesiva uns aos
outros. Ela lembrava que havia aprendido na escola que seria possível construir três dos
poliedros de Platão com aqueles triângulos. Ela construiu, com 4 triângulos, o tetraedro,
e com 20 triângulos, o icosaedro. Mas esqueceu qual era o terceiro poliedro regular
convexo que podia construir apenas com triângulos equiláteros. Esse poliedro é o
poliedro regular convexo que podia construir apenas com triângulos equiláteros. Esse
poliedro é o:
a) pentaedro.
b) hexaedro.
c) octaedro.
d) dodecaedro.
9) O GPS é um sistema que permite, por meio de satélites, obter as coordenadas em
latitudes e longitudes de um objeto na face da Terra. Se a leitura do GPS informa que
um objeto se encontra na latitude 22,5° e na longitude 38,7°, então, na figura seguinte
(que limita a tela de um radar) o objeto estará em:
a) Q1. b) Q11. c) Q9. d) Q4.
10) O pátio da escola de Pedro foi enfeitado com bandeirolas coloridas para a festa
junina. O professor de matemática encarregado dessa tarefa resolveu propor aos alunos
as seguintes condições para a confecção das bandeirolas:
1.Devem ser formadas por três faixas, como o modelo seguinte.
2.Para as faixas 1 e 3 devem ser usadas as cores Verde, Amarelo, Vermelho, ou Azul.
3.Para a faixa 2 podem-se usar apenas as cores Amarelo ou Vermelho.
4.Todas as bandeirolas deverão ter 3 cores distintas.
Antes de iniciar o trabalho, o professor propôs que os alunos descobrissem o número de
bandeirolas diferentes que poderiam ser obtidas com essas condições.
A turma, que resolveu corretamente o problema, descobriu que esse número é
a) 10.
b) 12.
c) 16.
d) 20.
Gabarito: 1) d 2) b 3) c 4) b 5) c 6) b 7) a 8) c 9) c 10) b









Nenhum comentário:
Postar um comentário