(A) a metade do preço de cada caneta.
(B) 1/7 do preço de cada caneta.
(C) 1/5 do preço de cada caneta.
(D) 1/14 do preço de cada caneta.
Resposta: B
02) Uma certa quantia deve ser distribuída entre três pessoas, de modo que a 2ª. pessoa receba a terça da 1ª.. Se a diferença entre a maior e a menor das partes é R$ 600,00, o valor de tal quantia é:
(A) R$ 1200,00
(B) R$ 1500,00
(C) R$ 1800,00
(D) R$ 2000,00
Resposta: C
03) O número que deve ser somado a ambos os termos da fração 2/7, de modo a obter-ser uma fração equivalente a 5/6, é:
(A) primo.
(B) fracionário.
(C) múltiplo de 3.
(D) divisível por 5:
Resposta: a
04) O número 5 é solução de qual das inequações seguintes?
Resposta: D
05) Dos números 7, 8, 9 e 10, qual ou quais são soluções da inequação ?
(B) só o 8
(C) 9 e 10
(D) só o 10
Resposta: A
06) Das inequações abaixo, a que aceita o número 3 como solução é:
Resposta: B
07) A soma da terça parte de um número com seu dobro é maior que 7. Este número pode ser:
(A) - 3
(B) 0
(C) 3
(D) 3,3
Resposta: D
08) A inequação 3 ( 1 - 2x ) + 5 ( 2x + 2 ) ≤ 7 tem as mesmas soluções que:
(A) - 6x + 10x ≥ 1 - 13
(B) 6x + 10x ≥ 7 = 13
(C) - 6x + 10x ≤ 7 - 13
(D) 6x - 10x ≥ - 7 + 13
Resposta: C
09) Se a é uma solução da inequação 3a + 6 ≥ a - 10, então:
(A) a ≥ 8
(B) a ≤ - 8
(C) a ≥ - 8
(D) a < 8
Resposta: C
10) O quádruplo de um número, somado a 5, é maior que o seu dobro subtraído de 9. Esse número é necessariamente:
(A) maior que 7.
(B) menor que 7.
(C) maior que -7.
(D) menor que -7.
Resposta: C
11) Se x é uma solução da inequação
, então:
(A) x ≥ - 2
(B) x ≤ - 2
(C) x ≥ 2
(D) x ≤ - 2
Resposta: B
PARA VOCÊ SABER MAIS SOBRE RESOLUÇÃO DE INEQUAÇÃO DO 1º GRAU ACESSE O LINK ABAIXO E ASSISTA O VÍDEO:




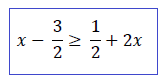
Bom exercicio.
ResponderExcluirObrigada, muito bom.
ResponderExcluirProf.pode me ajudar como resolver esta inequacao,que aceita o número 3como solução é a)x+1_<2/3..
ResponderExcluirx + 1 < 2/3
ResponderExcluir3(x+1)< 2
3x + 3 < 2
3x < 2 - 3
3x < -1
x< -1/3