> Resolva os seguintes problemas:
01) Calcule a soma dos quadrados das raízes da equação x² - 2x + 6 = 0, sem resolvê-la.
02) Calcule o valor de h na equação ( h + 3 )x² - 2(h + 1)x + h - 10 = 0, de modo que a soma dos inverso das raízes seja 1/3.
1/x' + 1/x" = 1/3 S = ( 2h + 2 )/( h + 3 ) P = (h - 10)/ (h + 3)
Resolvendo temos
(3x" + 3x' )/ 3( x' . x" ) = ( x' . x" )/ 3(x' . x" )
3 ( x" + x' ) = x' . x"
fazendo a substituição temos:
3( 2h + 2)/(h + 3 ) = ( h - 10)/( h +3 )
(6h + 6)/ (h = 3 ) = ( h - 10)/( h +3 )
6h + 6 = h - 10
6h - h = - 10 - 6
5h = - 16
h = -16/5
03) Dada a equação x² - 5 + q = 0, determine q, de modo que:
I) uma das raízes seja 3;
x' = 3
x² - 5x + q = 0
3² - 5. 3 + q = 0
9 - 15 + q = 0
- 6 + q = 0
q = 6
II) a soma dos inverso das raízes seja 5/4.
1/x' + 1/x"
(4x" + 4 x')/ 4(x'. x") = 5(x'. x")/4(x' . x")
4(x" + x' ) = 5( x' . x" ) Fazendo : S = 5 e P = q
4 . 5 = 5. q
20 = 5q
q = 20/5
q = 4
04) Determine c na equação x² - 10x + c = 0, de modo que uma raiz seja o quadruplo da outra.
x' = 4x" S =10
4x" - x' = 0
x" + x' = 10
5x" = 10
x" = 10/5
x" = 2
substituindo x" = 2 :
x² - 10x + c = 0
2² - 10.2 + c = 0
4 - 20 + c = 0
- 16 + c = 0
c = 16
05) Determine k na equação x² - 7x + k = 0, de modo que suas raízes sejam consecutivas.
x" - x' = 1 x² - 7x + k = 0
x" + x' = 7 4² - 7. 4 + k = 0
2x" = 8 16 - 28 + k = 0
x" = 8/2 - 12 + k = 0
x" = 4 k = 12
06) Determine a, de modo que uma das raízes de ax² - 8x + 3= 0 seja o triplo da outra.
x' = 3x" x' + x" = 8/a > 3x" + x" = 8/a
3/2 = 3x" x' . x" = 3/a 4x" = 8/a
6x" = 3 x' = 3/a . a/2 x" = 8/a . 1/4
x" = 3/6 x' = 3a/2a x" = 8/4a
x" = 1/2 x' = 3/2 x" = 2/a
ax² - 8x + 3 = 0
a(3/2)² - 8.3/2 + 3 = 0
9a/4 - 12 + 3 = 0
(9a - 48 + 12)4 = 0
9a - 36 = 0
9a = 36
a = 36/9
a = 4
07) Calcule o menor valor de m na equação mx² - ( 3m - 1 )x + m = 0, de modo que a razão entre suas raízes seja 1/4.
x'/x"=1/4 x' . x" = 1
4x' = x" x'. 2 = 1
4.1/2 = x" x' = 1/2
4/2 = x"
x" = 2
Substituindo x" = 2 em
mx² - ( 3m - 1 ) + m = 0
2²m - (3m - 1).2 + m = 0
4m - 6m + 2 + m = 0
5m - 6m + 2 = 0
- m = -2 (-1)
m = 2
08) determine m, de modo que uma das raízes da equação ( m - 1 )x² - 8x + 3 seja o inverso da outra.
x' = 1/x" x' + x" = 8/m -1
x' . x" = 1 x' . x" = 3/ m -1
substituindo em x' . x" = 1
3/m-1 = 1
m - 1 = 3
m = 3 = 1
m = 4

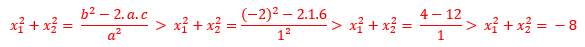
Nenhum comentário:
Postar um comentário